In Class Activity Plan
Week 14: Angular Motion & Simple Harmonic Motion
25 min������������ Whiteboard - Satellite Centripetal Ranking Problem (Word, Pdf)
����������������������� PURPOSE: Practice modeling centripetal acceleration situation.����� �����������
Lots of options here probably want to give one as homework:
20 min ����������� Board Meeting
PURPOSE: Build consensus around modeling centripetal acceleration situation.
Goals:
� Centripetal force is just the net force towards the center
� Need to attend to the radius of the circular path
Additional resources which could be used:
Ferris Wheel Centripetal Force (Word, Pdf)
Centripetal Force Ranking (Word, Pdf)
Circular Motion Problems (Word, Pdf)
20 min������������ Whiteboard - Ladybug revolution part 1
PURPOSE: Investigate rotational motion, introduce rotational analogs to translational kinematics
Direct students to PhET simulation � Ladybug Revolution (http://phet.colorado.edu/en/simulation/rotation)
����������������������� Give students 10 minutes to explore.
����������������������� Summarize what you have learned on whiteboard.
10 min������������ Board Meeting
����������������������� PURPOSE: Share what was learned from investigation of simulation
20 min������������ Whiteboard - Ladybug Revolution part 2
PURPOSE: Develop models for constant rotational motion from graphs of rotational motion.��
����������������������� Directions: Return to the Ladybug Revolution simulation
Use the second tab which shows graphs, use radians.
Answer: What have you learned? What rules can you make? What questions do you have?� On whiteboard.
20 min������������ Board Meeting
PURPOSE: Reach consensus about equations that describe constant angular acceleration motion.
1. Review the kinematic representations in the basic 1-d constant acceleration model
����������������������������������� a) Equations
����������������������������������������������� d = Δpos
����������������������������������������������� v = Δpos/Δt
����������������������������������������������� a = Δv/Δt
����������������������������������������������� d = v0 + �at2
����������������������������������������������� vf = v0 + at
����������� b) Velocity-time graph
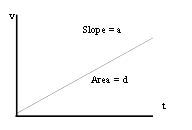
2. When does this model apply?
Answer: when we have straight line motion
3. What is the motion of the wheel?
Answer: not moving linearly, but it is movingt
����������� 4. Create a table of angular variables by analogy
|
d = Δpos |
θ = Δangle |
|
v = Δpos/Δt |
ω = Δangle/Δt |
|
a = Δv/Δt |
α = Δω/Δt |
|
d = v0 + �at2 |
θ = ωt + � α t |
|
vf = v0 + at |
ωf = ω0 + at |
5. How should be able to go between the two versions?
����������������������� a) d = r θ
b) v = r ω
c) a = r α
����������� 6. �Now we can add on the rest of relationships
�����������������������
|
m |
I = �miri |
|
p = mv |
L = Iω |
|
Fnet = m a |
t = Iα |
|
Eklinear = � m v2 |
Ekrot = � I ω2 |
25 min������������ Whiteboard- Helicopter Quantitative Problem (Word, Pdf)
����������������������� PURPOSE: Model situation with constant angular acceleration
�����������
20 min������������ Board Meeting����������
����������������������� PURPOSE: Build consensus about modeling constant angular acceleration
Homework - Ranking of Theta vs t graph (Word, Pdf) and Rotational speed ranking (Word, Pdf)